Ng Cheuk Fai

Ng Cheuk Fai

PhD candidate in Economics

Posts by Tags

Statistics

Bahr and Esseen Inequality

less than 1 minute read

Published:

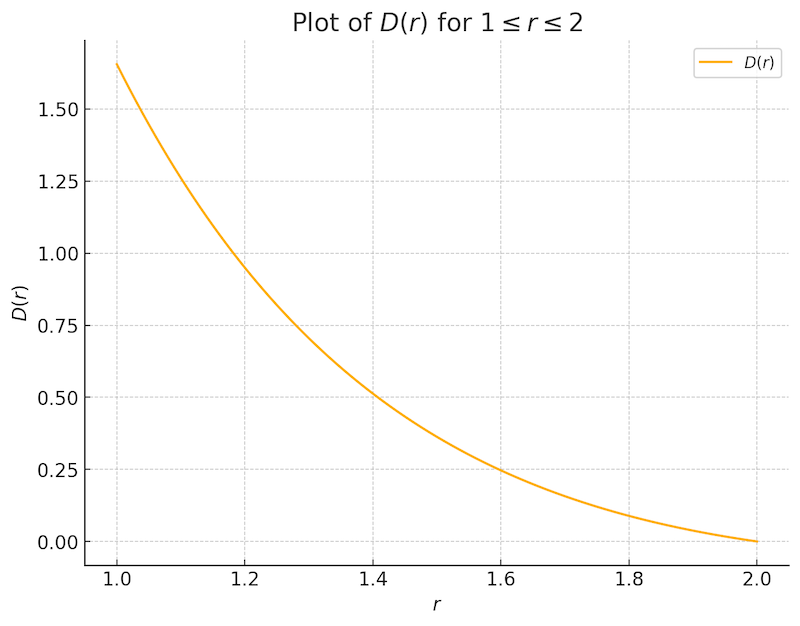
Bahr and Esseen (1965) Inequality provides a useful moment bound on the absolute sum of independent variable. It states as follows: let \(X_1,X_2,\ldots , X_n\) be a sequence of independent r.v.’s with \(EX_i=0\) and \(E|X_i|<\infty,1\leq i\leq n.\) If \(r\) satisfies \(\begin{aligned} D(r)=\frac{13.52}{(2.6 \pi)^r}\Gamma(r)\sin (r\pi/2)<1 \text{ and } 1\leq r \leq 2, \end{aligned}\) then \(E|\sum^n_{i=1}X_i|^r\leq \frac{1}{1-D(r)}\sum^n_{i=1}|X_i|^r.\)

Below is a plot of \(D(r)\).

Stein's Method

less than 1 minute read

Published:

Stein’s method is a way to show that a random variable \(W\) has a distribution that is close to a target distribution (usually the normal distribution). Its idea is that if two random variables are similar, then the expectations of some functions of the two random variables being compared should be similar.

calculus

Gamma functions

less than 1 minute read

Published:

Recall the factorial function of a non-negative integer \(n\) is given by \(\begin{aligned} n!=n\times (n-1)\times (n-2)\times (n-3)\times \cdots \times 2\times 1 \end{aligned}\) and the binomial coefficients are given by \(\begin{aligned} \begin{pmatrix} n\\ k \end{pmatrix} = \frac{n!}{k!(n-k)!} \end{aligned}\)

Absolute Continuities

less than 1 minute read

Published:

Absolutely continuity is particularly useful in statistics because any function that is absolute continuous must be differentiable almost everywhere and satisfies the fundamental theorem of calculus. As a result, any random variable that has an absolute continuous density function will be a continuous random variable.

graphs

Activation Functions

less than 1 minute read

Published:

Here are some graphs of common activation functions.