Sitemap
A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.
Pages
Posts
Gamma functions
Published:
Recall the factorial function of a non-negative integer \(n\) is given by \(\begin{aligned} n!=n\times (n-1)\times (n-2)\times (n-3)\times \cdots \times 2\times 1 \end{aligned}\) and the binomial coefficients are given by \(\begin{aligned} \begin{pmatrix} n\\ k \end{pmatrix} = \frac{n!}{k!(n-k)!} \end{aligned}\)
Absolute Continuities
Published:
Absolutely continuity is particularly useful in statistics because any function that is absolute continuous must be differentiable almost everywhere and satisfies the fundamental theorem of calculus. As a result, any random variable that has an absolute continuous density function will be a continuous random variable.
Activation Functions
Published:
Here are some graphs of common activation functions. 
Bahr and Esseen Inequality
Published:
Bahr and Esseen (1965) Inequality provides a useful moment bound on the absolute sum of independent variable. It states as follows: let \(X_1,X_2,\ldots , X_n\) be a sequence of independent r.v.’s with \(EX_i=0\) and \(E|X_i|<\infty,1\leq i\leq n.\) If \(r\) satisfies \(\begin{aligned} D(r)=\frac{13.52}{(2.6 \pi)^r}\Gamma(r)\sin (r\pi/2)<1 \text{ and } 1\leq r \leq 2, \end{aligned}\) then \(E|\sum^n_{i=1}X_i|^r\leq \frac{1}{1-D(r)}\sum^n_{i=1}|X_i|^r.\)
Below is a plot of \(D(r)\). 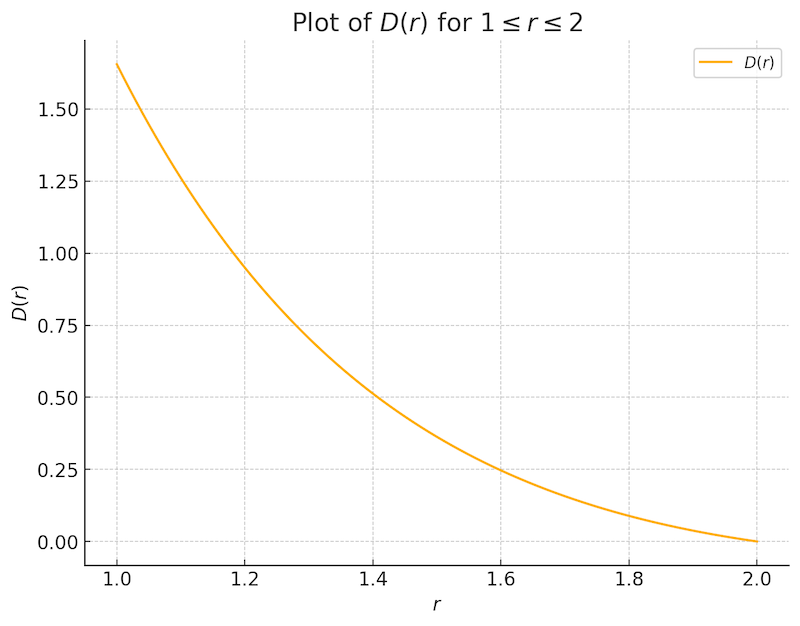
Stein's Method
Published:
Stein’s method is a way to show that a random variable \(W\) has a distribution that is close to a target distribution (usually the normal distribution). Its idea is that if two random variables are similar, then the expectations of some functions of the two random variables being compared should be similar.
portfolio
Portfolio item number 1
Short description of portfolio item number 1
Portfolio item number 2
Short description of portfolio item number 2 
publications
VCE_MCOV: Stata module to compute the Leave-Cluster-Out-Crossfit (LCOC) variance estimates for user-chosen coefficients in a linear regression model
Published in Statistical Software Components S459293, 2024
vce_mcov is an eclass command that can be used after running reg. It replaces the entries of the variance matrix (stored in e(V)) relating to user-chosen parameter(s) of inferential interest with the Leave-Cluster-Out-Crossfit (LCOC) estimates (see Anatolyev and Ng, 2024). All postestimation commands will work as usual.
Recommended citation: Stanislav Anatolyev & Cheuk Fai Ng (2024). "VCE_MCOV: Stata module to compute the Leave-Cluster-Out-Crossfit (LCOC) variance estimates for user-chosen coefficients in a linear regression model," Statistical Software Components S459293.
Many-covariate and cluster robust estimation and inference
Published in , 2024
Recommended citation: Stanislav Anatolyev & Cheuk Fai Ng (2024). "Many-covariate and cluster robust estimation and inference"
Instrumental variables estimation with many instruments using Thresholding
Published in , 2024
Recommended citation: Cheuk Fai Ng (2024). "Instrumental variables estimation with many instruments using Thresholding"
talks
Talk 1 on Relevant Topic in Your Field
Published:
This is a description of your talk, which is a markdown files that can be all markdown-ified like any other post. Yay markdown!
Conference Proceeding talk 3 on Relevant Topic in Your Field
Published:
This is a description of your conference proceedings talk, note the different field in type. You can put anything in this field.
teaching
Teaching experience 1
Undergraduate course, University 1, Department, 2014
This is a description of a teaching experience. You can use markdown like any other post.
Teaching experience 2
Workshop, University 1, Department, 2015
This is a description of a teaching experience. You can use markdown like any other post.
